Les éléments de base des statistiques expliqués

Probabilités élémentaires

La distribution normale

L’un des outils statistiques les plus pertinents est la distribution normale et le mot “écart-type”.
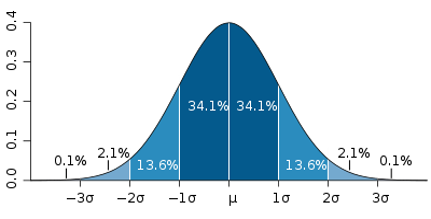
La distribution normale est le terme associé à la courbe de probabilité en forme de cloche illustrée ci-dessous. Cette courbe décrit le lien entre la probabilité et l’incident.

µ = Le signe micro dénote la valeur moyenne de tous les incidents.
σ = La lettre grecque sigma désigne un écart-type.

Il est défini que les nombres/incidents dans une population se répartissent comme suit :

+/- 1 sigma = 68,2 % de la population
+/- 2 sigma = 95,4 % de la population
+/- 3 sigma = 99,7 % de la population

Exemple :
Vous avez acheté une boîte de 100 pommes de 65 mm. Les petits caractères indiquent (1 sigma 2 mm) après 65 mm. Il est clair que toutes les pommes ne sont pas de taille identique, que pouvez-vous attendre de cette boîte ? La taille moyenne (µ) sera de 65 mm !

(34,1 % + 34,1 % =) 68,2 % * 100 pommes = 68 pommes seront à 65 mm +/- 1 sigma (σ) ( +/- 2 mm) Certaines 63 mm d’autres 67 mm.
(13,6+13,6 =) 27,2% * 100 pommes = 27 pommes seront à plus de 2 mais moins de 4 mm de la moyenne de 65 mm.
(2,1 + 2,1 =) 4,2% * 100 pommes = 4-5 pommes seront à plus de 4 mm de la moyenne.
Pire encore, 2 pommes sur 1000 DOIVENT être très éloignées de la moyenne pour que les autres chiffres soient vrais.
Ce type de statistiques s’applique également aux nombres analytiques.

Termes analytiques

Les statistiques jouent un rôle très important dans la description des performances d’une méthode analytique.
Il peut être utile, pour une description complète des performances, d’inclure au moins certains des éléments suivants en termes statistiques :

Les traditions et les écoles utilisent des mots différents pour désigner les mêmes choses et parfois des choses différentes.
Les mots qui décrivent dans quelle mesure vous êtes en moyenne proche des bonnes valeurs sont les suivants

• Précision
• Accord

Mots décrivant les résultats obtenus avec la même méthode sur des éléments d’essai identiques dans le même laboratoire par le même opérateur utilisant le même équipement dans de courts intervalles de temps.

• Répétabilité
• Stabilité à court terme
• Précision

Mots décrivant les résultats obtenus avec la même méthode dans différents laboratoires par différents opérateurs utilisant différents équipements

• Reproductibilité
• Stabilité à long terme

Pour décrire une méthode, il faut inclure un terme des trois groupes, nous continuerons ici à utiliser les termes accord, répétabilité et reproductibilité.

Accord

Une méthode NIR est une méthode secondaire qui dépend à 100 % de la méthode primaire utilisée pour l’étalonnage. Le terme “accord” décrit le degré d’accord entre la méthode NIR et la méthode de référence. Il est souvent représenté graphiquement de la manière suivante.

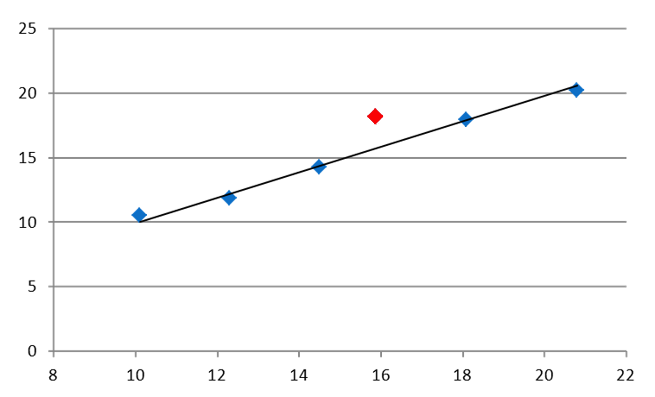
La flèche rouge indique un échantillon qui n’est pas “d’accord” à 100 %, mais qui a raison et qui a tort ?

Les deux méthodes contribuent à l’erreur. Quantifiez les deux avant de juger une méthode.

Dans l’exemple, la concordance est exprimée en termes statistiques par 1 sigma = 0,38, ce qui signifie que la méthode NIR concorde avec la méthode primaire dans 68 % des cas à +/- 0,38 et dans 99,7 % des cas à +/- 1,14 (3 sigma) et que, l’échantillon se trouvant dans ces limites, la concordance est bonne.

Répétabilité

La répétabilité est un paramètre très important dans la description d’une méthode, puisqu’il s’agit de la capacité à répéter le même nombre plusieurs fois de suite dans une certaine plage définie (que l’on espère petite). Pour un analyseur en ligne, cela peut se traduire par la plus petite variation de production détectable par l’analyseur.

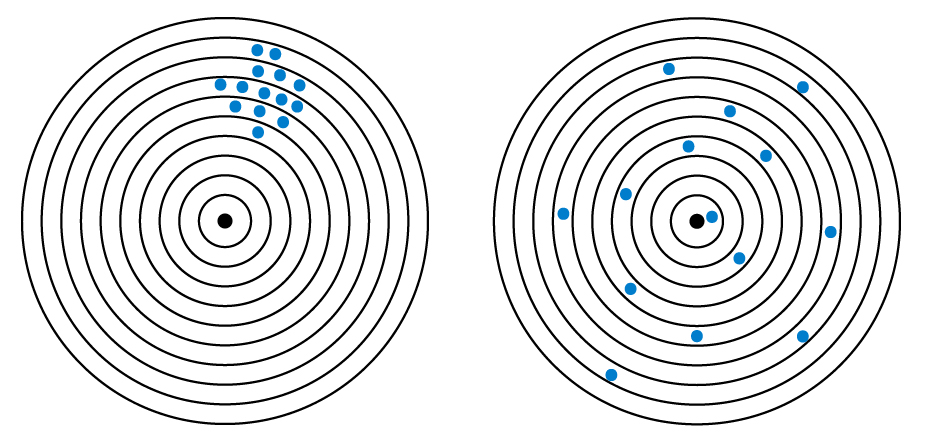
Regardez le tir sur cible ci-dessous.
Cas A : Très reproductible, pas très précis
Cas B : Faible répétabilité, accord élevé (en moyenne)

Les deux problèmes nécessitent des remèdes très différents et seul un scénario bien documenté peut être corrigé.

Reproductibilité

La reproductibilité est liée à la répétabilité, mais plutôt que de laisser l’échantillon en place et de l’analyser dix fois afin de tester la stabilité à court terme du matériel, nous nous efforçons de tester la robustesse de la méthode afin de répondre à des questions comme celles-ci :

• Aurai-je la même réponse demain ?
• Une autre personne obtiendra-t-elle le même résultat ?
• Est-ce que j’obtiendrai la même chose dans un autre contenant d’échantillon (bocal, pétri, flacon) ?
• Que se passe-t-il si j’emballe 5 échantillons à partir du même échantillon principal ?

Le seul moyen de savoir est de tester !

Il convient de noter que l’accord est affecté par une répétabilité et une reproductibilité médiocres et qu’une bonne règle empirique est que les paramètres de stabilité ne doivent pas dépasser 33 % de l’accord, c’est-à-dire que dans l’exemple d’un écart-type de 0,38, la “dispersion” des mesures répétées doit être inférieure à (0,38*/3 = 0,13). Un écart-type de stabilité de 0,13 suit les mêmes règles que tout autre écart-type : 1 sigma = 0,13 !

Exemple pratique

Un analyseur NIR analyse les aliments pour poulets. Dans cet exemple, nous nous concentrons sur le composant Graisse. L’analyse de 10 échantillons avec l’analyseur et le laboratoire de référence donne le tableau de résultats ci-dessous.

NIR fat (%)	Lab fat (%)	Difference (%)
12,65	12,92	0,27
13,11	12,79	-0,32
8,93	8,67	-0,26
13,17	13,36	0,19
12,22	12,17	-0,05
11,88	12,12	0,24
12,79	13,19	0,4
11,03	11,41	0,38
	Average deviation (µ)	0,106 (%)
	Standard deviation	0,263 (%)

À première vue, cela ne semble pas très bon et nous devons donc creuser davantage pour comprendre les statistiques et les sources d’erreur.

La valeur moyenne de 0,106 pourrait être interprétée comme une erreur systématique, c’est-à-dire que le laboratoire est en moyenne 0,106 % plus élevé que l’analyseur NIR. Cette interprétation est cependant loin d’être certaine, car la moyenne est calculée sur 8 résultats seulement et le “biais” est inférieur à 50 % de l’accord ; il est donc peu probable qu’il soit ce que les statistiques appellent “significatif”. Pour déterminer un biais/une erreur systématique, il faut disposer de plus de chiffres sur la durée et effectuer un véritable calcul de signification (non abordé dans cette introduction).

La première étape consiste à étudier la contribution de la répétabilité. Nous laissons simplement un échantillon dans l’analyseur et l’analysons 8 fois.

Repeat	Fat (%)
1	12,58
2	12,71
3	12,72
4	12,60
5	12,77
6	12,74
7	12,69
8	12,79
Repeatability (σ)	0,07

Erreur d’échantillonnage

Cette erreur couvre de multiples défaillances dans le processus analytique, depuis l’échantillonnage primaire jusqu’au simple fait que l’analyseur NIR et la méthode de référence ne voient pas, de facto, le même échantillon.

Dans ce petit exemple, nous nous concentrons sur la partie de l’erreur d’échantillonnage liée à la reproductibilité de la manipulation et à l’hétérogénéité, qui peut être observée en remplissant la coupelle de l’analyseur, disons 8 fois, à partir du même échantillon primaire et en effectuant l’analyse. Si l’échantillon est parfaitement homogène, les résultats seront tous identiques, mais c’est très rarement le cas, et cela s’explique par le fait que les analyseurs NIR voient un échantillon et la méthode de référence un autre.

Sample replicate	Fat (%)
1	12,81
2	12,63
3	12,69
4	12,63
5	12,77
6	12,87
7	12,79
8	12,54
Reproducibility (σ)	0,10

Budget d’erreur

Nous pouvons maintenant établir un budget d’erreurs et juger les résultats sur cette base. De cette manière, le contrôle statistique d’un analyseur donné devient un calcul et non un sentiment.

Les trois principales contributions à l’accord NIR sont les suivantes

• a = Méthode de référence
• b = Erreur d’échantillonnage
• c = Répétabilité

Les mathématiques permettent d’obtenir une approximation des contributions comme suit

Accord STD dev ≈ (a 2 +b 2 +c 2 )½
Nous savons que a = 0,23
Nous savons que c = 0,07
Nous savons que b = 0,1

Les sources d’erreur connues sont réparties de la sorte et il est évident que la méthode de référence joue un rôle important.

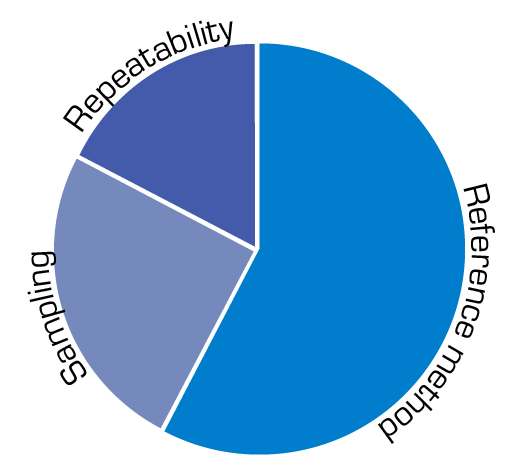
a ² +b ² +c ² = (0.23)² + (0.07) ² + (0.1) ² ≈ 0.26 %

Conclusion

L’accord observé entre la méthode de référence et l’analyseur NIR correspond au budget d’erreur calculé et nous disons que l’analyseur est en contrôle statistique puisque l’erreur peut être expliquée.

Si l’on souhaite améliorer la méthode, il faut cibler la méthode de référence car c’est elle qui aura l’effet le plus important sur le résultat.

Carte de contrôle

Une carte de contrôle est un outil de visualisation graphique permettant de suivre l’évolution des erreurs statistiques dans le temps. Si une méthode fait partie d’un processus de contrôle critique ou d’un élément vital pour maintenir le revenu au bon niveau, il est essentiel de continuer à suivre l’accord afin de mener les processus aussi près que possible de l’objectif.

La perte d’un accord est synonyme de perte de profit.

Vous trouverez ci-dessous un exemple typique de diagramme de contrôle pour l’accord sur la détermination des matières grasses dans le lait cru. Même de petites déviations sont susceptibles de coûter de l’argent ou de nuire à la qualité du produit.

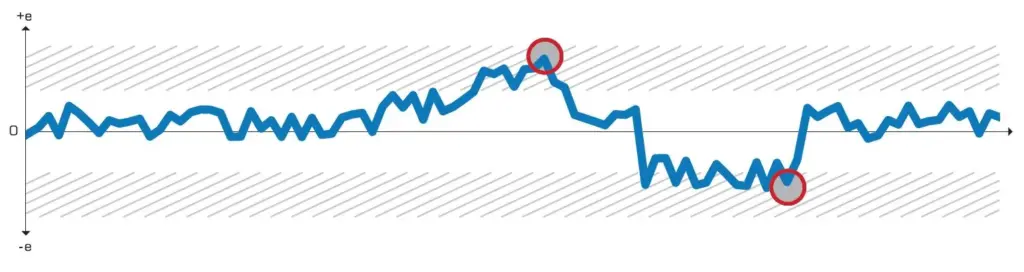
Une carte de contrôle se caractérise par des données tracées dans le temps. Les données ont une ligne centrale et un ou plusieurs ensembles de limites de contrôle supérieures et inférieures. Tant que les données oscillent entre les limites supérieures et inférieures, aucun ajustement n’est effectué, car le processus ou le résultat sont considérés comme “sous contrôle”. Si l’on procède à des ajustements sur la base d’un seul résultat, il en résulte des biais importants et un processus qui s’écarte de l’objectif.